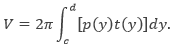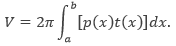PERTEMUAN 11 (INTEGRAL FUNGSI RASIONAL)

INTEGRAL FUNGSI RASIONAL

Fungsi rasional adalah fungsi yang berbentuk pecahan dimana pembilang dan penyebutnya masing-masing merupakan fungsi polinomial. Menurut konsep kesamaan polinom jika ruas kiri sama dengan ruas kanan maka suku-suku sejenisnya adalah sama.

LATIHAN SOAL MODUL  PERTEMUAN 11

NAMA : SHEILLINA RICHIE FEBRYANTI

NIM : 191011402734

KELAS/RUANG : 02TPLP024/V205

KALKULUS II

PERTEMUAN 18 (VOLUME BIDANG PUTAR DENGAN MERODE CINCIN)

VOLUME BIDANG PUTAR DENGAN MERODE CINCIN

Pembahasan sebelumnya telah dibahas tentang bagaimana menentukan volume benda putar dengan menggunakan metode cakram. Metode cakram tersebut dapat diturunkan menjadi metode yang lain, yaitu metode cincin (washer method), yaitu suatu metode yang menggunakan integral dalam menentukan volume benda putar yang memiliki lubang. Cincin dalam metode ini dibentuk oleh hasil putaran persegi panjang terhadap sumbu putaran tertentu (sumbu putaran tidak berimpit dengan sisi persegi panjang), seperti terlihat pada gambar berikut.

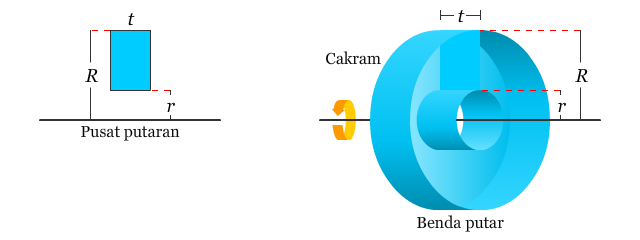
Jika r dan R secara berturut-turut merupakan jari-jari dalam dan luar dari cincin dan t merupakan ketebalan cincin, maka volumenya dapat ditentukan sebagai berikut.

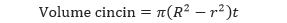
Untuk mengetahui bagaimana konsep ini dapat digunakan untuk menentukan volume benda putar, perhatikan daerah yang dibatasi oleh jari-jari luar R(x) dan jari-jari dalam r(x), seperti yang ditunjukkan gambar di bawah ini.

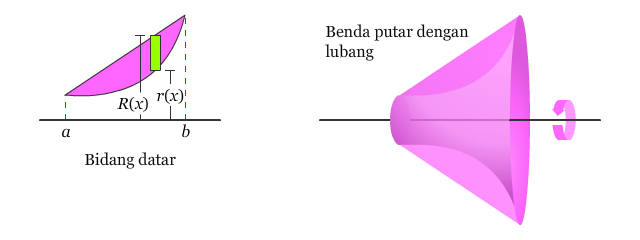
Jika daerah tersebut diputar menurut sumbu putar yang diberikan, volume benda putar yang dihasilkan adalah

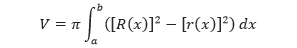
Perhatikan bahwa integral yang melibatkan jari-jari dalam merepresentasikan volume lubang yang dikurangkan dari integral yang melibatkan jari-jari luar. Untuk lebih memahami dalam menemukan volume benda putar dengan metode cincin, perhatikan contoh berikut.

Contoh: Penggunaan Metode Cincin

Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh grafik dari y = √x dan y = x2 terhadap sumbu-x, seperti yang ditunjukkan oleh gambar berikut.

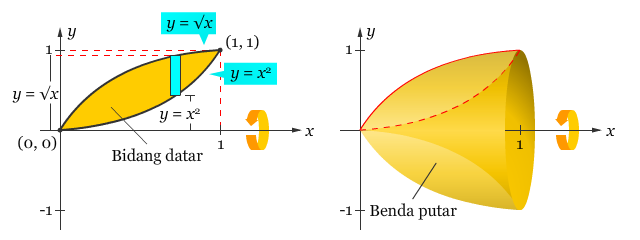
Pembahasan Dari gambar di atas dapat ditentukan bahwa jari-jari luar dan dalamnya adalah sebagai berikut.

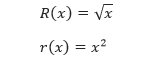
Dengan mengintegralkan dengan batas antara 0 dan 1, menghasilkan

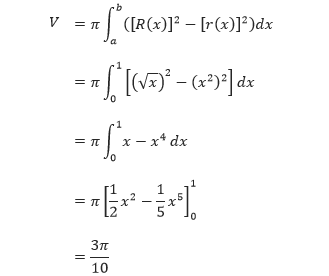
PERTEMUAN 17 (VOLUME BIDANG PUTAR DENGAN METODE KULIT TABUNG)

VOLUME BIDANG PUTAR DENGAN METODE KULIT TABUNG

Pada bagian ini akan dibahas mengenai metode alternatif dalam menentukan volume benda putar. Metode ini disebut metode kulit tabung (shell method) karena metode ini menggunakan volume dari kulit tabung. Perhatikan persegi panjang di bawah ini dengan t adalah panjang dari persegi panjang, l adalah lebar persegi panjang, dan p adalah jarak antara sumbu putaran dengan pusat dari persegi panjang.

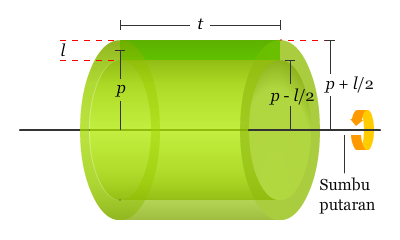
Ketika persegi panjang tersebut diputar menurut sumbu putarannya maka akan dihasilkan kulit tabung dengan ketebalan l. Untuk menentukan volume kulit tabung tersebut, perhatikan dua tabung (tabung luar dan dalam) yang nampak pada gambar di atas. Jari-jari tabung yang lebih besar merupakan jari-jari luar dari kulit tabung, dan jari-jari dari tabung yang lebih kecil merupakan jari-jari dalam dari kulit tabung. Karena p adalah rata-rata dari jari-jari kulit tabung, dan diketahui bahwa jari-jari luarnya p + l/2 dan jari-jari dalamnya p – l/2.

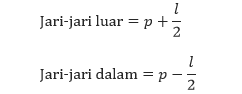
Maka, volume dari kulit tabung adalah

Rumus di atas dapat digunakan untuk menentukan volume dari benda putar. Anggap bidang datar pada gambar di bawah diputar menurut sumbu putarnya sehingga dihasilkan suatu benda putar.

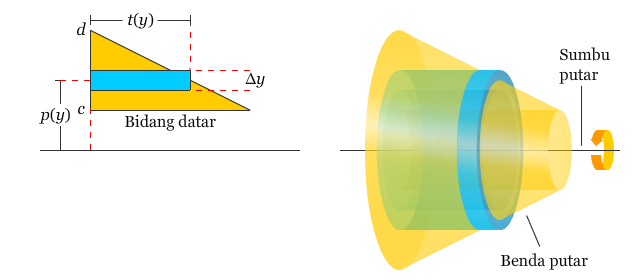
Apabila diperhatikan lebar dari persegi panjang tersebut adalah Δy, maka persegi panjang yang diputar terhadap garis yang sejajar dengan sumbu-x akan menghasilkan suatu kulit tabung yang volumenya

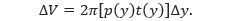
Volume dari benda putar di atas dapat didekati dengan menggunakan volume n kulit tabung yang tebalnya Δy, tinggi t(yi) dan rata-rata jari-jarinya p(yi).

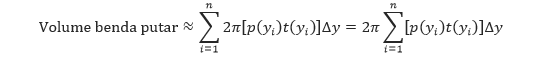
Pendekatan ini akan semakin baik dan semakin baik jika ||Δ|| → 0 atau n → ∞. Sehingga, volume benda putar tersebut adalah

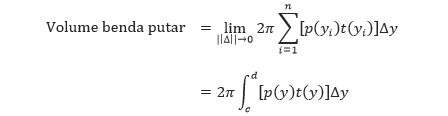
METODE KULIT TABUNG
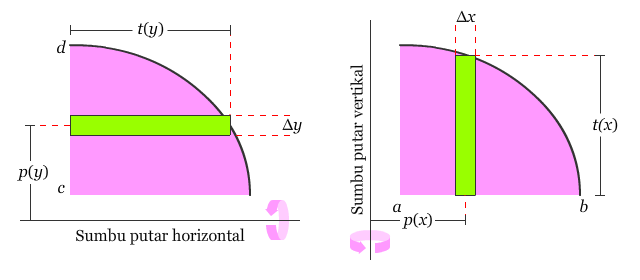
Untuk menentukan volume benda putar dengan metode kulit tabung, gunakan salah satu dari rumus berikut, seperti yang ditunjukkan oleh gambar di bawahnya.
Sumbu putarnya horizontal,

Sumbu putarnya vertikal,

Contoh I: Penggunaan Metode Kulit Tabung untuk Menentukan Volume

Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh

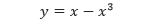
dan sumbu-x (0 ≤ x ≤ 1) dengan sumbu putarannya adalah sumbu-y.

Pembahasan Karena sumbu putarannya vertikal, gunakan persegi panjang vertikal, seperti yang ditunjukkan oleh gambar di bawah.

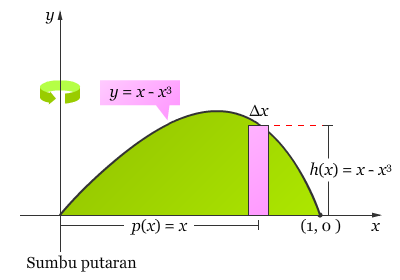
Ketebalan Δx mengindikasikan bahwa x merupakan variabel dalam proses integrasi yang akan dilakukan. Jarak antara pusat persegi panjang dengan sumbu putaran adalah p(x) = x, dan tingginya adalah

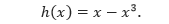
Karena rangenya antara 0 sampai 1, maka volume benda putar yang terbentuk dapat ditentukan sebagai berikut.

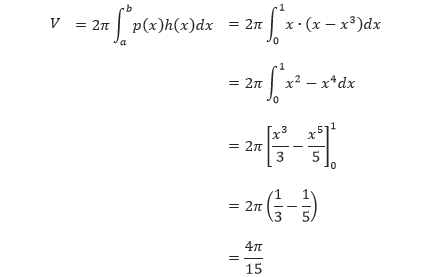
PERTEMUAN 14 (LUAS DAERAH YANG DI BATASI SUMBU X DAN Y)

LUAS DAERAH YANG DI BATASI SUMBU X DAN Y

A.  MENENTUKAN LUAS DAERAH

1. Menentukan Luas Daerah di Atas Sumbu -x

Pada subbab sebelumnya, kita telah mengetahui bahwa luas merupakan limit suatu jumlah, yang kemudian dapat dinyatakan sebagai integral tertentu. Pada subbab ini, akan dikembangkan pemahaman untuk menentukan luas daerah yang dibatasi oleh beberapa kurva.

Misalkan R daerah yang dibatasi oleh kurva y = f(x), sumbu -x, garis x = a, dan garis x = b, dengan f(x) >= 0 pada

[a, b], maka luas daerah R.

Luas Daerah di Atas Sumbu-x

Luas daerah yang dibatasi kurva y = f(x), sumbu-x, garis $x=a$ dan $x=b$

dengan $f\left(x\right)\ge 0$ pada $[a,b]$ adalah :$$L={\int }_a^{b}f\left(x\right)dx$$

Luas Daerah di Bawah Sumbu-x

Luas daerah yang dibatasi kurva y = f(x), sumbu-x, garis $x=a$ dan $x=b$ dengan $f\left(x\right)\le 0$ pada $[a,b]$ adalah : $$L=-{\int }_a^{b}f\left(x\right)dx$$

Luas Antara Dua Kurva

Luas daerah yang dibatasi kurva $y=f\left(x\right)$, $y=g\left(x\right)$, garis $x=a$ dan $x=b$ dengan $f\left(x\right)\ge g\left(x\right)$ pada $[a,b]$ adalah : $$L={\int }_a^b\left(f\left(x\right)-g\left(x\right)\right)dx$$

LATIHAN SOAL MODUL PERTEMUAN 14